ಅವಿಚ್ಛಿನ್ನತೆ

ಗಣಿತ ಉತ್ಪನ್ನಗಳ (ಮ್ಯಾಥ್‍ಮ್ಯಾಟಿಕಲ್ ಫಂಕ್ಷನ್ಸ್) ಒಂದು ಮುಖ್ಯ ಆಧಾರಭೂತ ಗುಣ (ಕಂಟಿನ್ಯೂಯಿಟಿ). ಈ ಅವಿಚ್ಛಿನ್ನತಾ ಗುಣವಿದ್ದರೆ ಉತ್ಪನ್ನ ಸ್ವಾಭಾವಿಕ ಲಕ್ಷಣವುಳ್ಳದ್ದೆಂದೂ ಇಲ್ಲದಿದ್ದರೆ ವಿಕಾರಯುಕ್ತವಾದದ್ದೆಂದೂ ಹೇಳಬಹುದು. ಅವಿಚ್ಛಿನ್ನತೆಯ ಅರ್ಥ ಉತ್ಪನ್ನದ ನಕ್ಷೆಯಿಂದ ಸ್ಪಷ್ಟವಾಗಿ ದೊರಕುತ್ತದೆ ಎಂಬ ಉತ್ಪನ್ನದ ನಕ್ಷೆ ಎಲ್ಲಿಯೂ ತುಂಡಾಗದೆ ಮೃದು ರೇಖೆಯಾಗಿದ್ದರೆ, ಉತ್ಪನ್ನ ಎಲ್ಲೆಡೆಯಲ್ಲಿಯೂ ಅವಿಚ್ಛಿನ್ನತೆಯಿಂದ ಕೂಡಿರುವುದು. ರೇಖೆ ಅಲ್ಲಲ್ಲೇ ತುಂಡಾಗಿದ್ದರೆ ಆ ಸ್ಥಳಗಳಲ್ಲಿ ಉತ್ಪನ್ನ ವಿಚ್ಛಿನ್ನತೆಯಿಂದ (ಡಿಸ್‍ಕಂಟಿನ್ಯೂಯಿಟಿ) ಕೂಡಿದೆ. ಸ್ವಲ್ಪ ಕೃತ್ರಿಮ ರೂಪದ ಒಂದು ಉದಾಹರಣೆಯಿಂದ ಇದನ್ನು ಸ್ಪಷ್ಟಪಡಿಸಬಹುದು. x ಸಂಖ್ಯೆಯ ಪೂರ್ಣಾಂಕ ಭಾಗ I (x) ಆಗಿರಲಿ. ಉತ್ಪನ್ನದ ನಕ್ಷೆ ಎಳೆದರೆ, ಆದಾಗ, ರೇಖೆ x=ಂ ಎಂಬ x—ಅಕ್ಷದ ಭಾಗವಾಗಿಯೂ ಆದಾಗ, x=1 ಎಂಬ ಸರಳ ರೇಖೆಯ ಭಾಗವಾಗಿಯೂ ಆದಾಗ, x=2 ಎಂಬ ಸರಳ ರೇಖೆಯ ಭಾಗವಾಗಿಯೂ ಇತ್ಯಾದಿಯಾಗಿ ಮುಂದುವರಿಯುವುದು. ಆದ್ದರಿಂದ x=1,x=2,x=3 ಇತ್ಯಾದಿ ಬೆಲೆಗಳನ್ನು ಹೊಂದಿರುವ ಬಿಂದುಗಳಲ್ಲಿ ನಕ್ಷೆ ಥಟ್ಟನೆ ಮೇಲಕ್ಕೆ ನೆಗೆಯುತ್ತದೆ. ಹೀಗೆ ನಕ್ಷೆ ಒಡೆದ ಚೂರು ಚೂರು ಸರಳರೇಖೆಗಳ ಸಮುದಾಯ. ಈ ಬಿಂದುಗಳ ಹೆಸರು ಉತ್ಪನ್ನದ ವಿಚ್ಛಿನ್ನತೆಯ ಬಿಂದುಗಳು.

The function $f(x)={\tfrac {1}{x}}$ is continuous on its whole domain $\mathbb {R} \setminus \{0\}$, but is not continuous over the domain $\mathbb {R}$ because it is discontinuous at $x=0$

ವ್ಯಾಖ್ಯೆ

ನಕ್ಷೆಯ ಚಿತ್ರದ ಆಧಾರದ ಮೇಲೆಯೇ ಅವಿಚ್ಛಿನ್ನತೆಯ ನಿಖರವಾದ ವ್ಯಾಖ್ಯೆಯನ್ನೀಗ ಕೊಡಬಹುದು : x=ಚಿ ಒಂದು ದತ್ತಬೆಲೆ. ಎಂಬುದು ಯಾವುದೇ ಧನಸಂಖ್ಯೆ ಇರುವಾಗ ಆಗತಕ್ಕ x ನ ಬೆಲೆಗಳಿಗೆಲ್ಲ ಆಗಿದ್ದರೆ, ಜಿ (x) ಉತ್ಪನ್ನ ಚಿ ಬಳಿ ಅವಿಚ್ಛಿನ್ನತೆಯನ್ನು ಪಡೆದಿದೆ.

ಮಿತಿ (ಲಿಮಿಟ್) ವ್ಯಾಖ್ಯೆಯೊಡನೆ ಇದನ್ನು ಸೇರಿಸಿ ಅವಿಚ್ಛಿನ್ನತೆಯ ವ್ಯಾಖ್ಯೆಯನ್ನು ಕೆಳಕೊಂಡಂತೆಯೂ ಬರೆಯಬಹುದು : ಜಿ (x) ಉತ್ಪನ್ನ ಚಿ ಬಳಿ ಅವಿಚ್ಛಿನ್ನತೆಯನ್ನು ಪಡೆಯಲು

1. ಜಿ (ಚಿ) ಪರ್ಯಾಪ್ತ (ಫೈನೈಟ್) ಸಂಖ್ಯೆಯಾಗಿರಬೇಕು; ಮತ್ತು
2. ಈ ಗುಣಗಳು ಚಿ ಬಿಂದುವಿನ ಒಂದು ಪಾಶ್ರ್ವದಲ್ಲಿ ಮಾತ್ರ ಇರುವುದಾದರೆ, ಉತ್ಪನ್ನ ಅರ್ಧ ಅವಿಚ್ಛಿನ್ನತೆಯಿಂದ ಕೂಡಿದೆ ಎನ್ನುತ್ತೇವೆ. ಮೊದಲಿನ ವ್ಯಾಖ್ಯೆಯಲ್ಲಿ, ಆದಾಗ ಆಗಿದ್ದರೆ, ಚಿ ಬಿಂದುವಿನ ಬಳಿ ಅವಿಚ್ಛಿನ್ನತೆ ಇರುವುದು. ಎರಡನೆಯ ವ್ಯಾಖ್ಯೆಯಲ್ಲಿ, ಇದಕ್ಕೆ ಆವಶ್ಯಕ. ಹೀಗೆಯೇ ಎಡಪಾಶ್ರ್ವದ ಅವಿಚ್ಛಿನ್ನತೆಯನ್ನು ವ್ಯಾಖ್ಯಿಸಬಹುದು. ಬಿಂದುವಿನ ಎರಡೂ ಪಾಶ್ರ್ವಗಳಲ್ಲಿ ಅವಿಚ್ಛಿನ್ನತೆಯಿದ್ದರೆ ಮಾತ್ರ, ಉತ್ಪನ್ನ ಅವಿಚ್ಛಿನ್ನತೆಯ ಗುಣ ಹೊಂದಿರುತ್ತದೆ. x = I (x) ಉತ್ಪನ್ನದ ನಕ್ಷೆಯಲ್ಲಿ x=1, x=2 ಮುಂತಾದ ಸ್ಥಳಗಳಲ್ಲಿ ಉತ್ಪನ್ನಕ್ಕೆ ಎಡಪಾಶ್ರ್ವದಲ್ಲಿ ಅವಿಚ್ಛಿನ್ನತೆ ಇದೆ, ಬಲಪಾಶ್ರ್ವದಲ್ಲಿ ಇಲ್ಲ.

ಒಂದು ದತ್ತ ಬಿಂದುವಿನಲ್ಲಿ ಒಂದು ಅವಿಚ್ಛಿನ್ನತೆಯನ್ನು ವ್ಯಾಖ್ಯಿಸಿರುತ್ತೇವೆ. ಒಂದು ಅಂತರ (ಚಿ,b ) ಯ ಎಲ್ಲ ಬಿಂದುಗಳಲ್ಲೂ ಜಿ (x) ಗೆ ಅವಿಚ್ಛಿನ್ನತೆ ಇರುವುದಾದರೆ, ಜಿ (x) ಉತ್ಪನ್ನ (ಚಿ,b ) ಅಂತರದಲ್ಲಿ ಅವಿಚ್ಛಿನ್ನತೆಯನ್ನು ಪಡೆದಿರುವುದು ಎನ್ನುತ್ತೇವೆ.

ವಿಚ್ಛಿನ್ನತೆ ಬರಬೇಕಾದರೆ, (i) ಜಿ (ಚಿ) ಪರ್ಯಾಪ್ತ ಸಂಖ್ಯೆಯಾಗಿಲ್ಲದೆ ಇರಬಹುದು, ಎಂದರೆ ಜಿ (ಚಿ) ಅನಂತವಾಗಿರಬಹುದು. ಅಥವಾ ಜಿ (ಚಿ) ಗೆ ಬೆಲೆಯೇ ಇಲ್ಲದಿರಬಹುದು. (ii) ಅಥವಾ ಬಲಗಡೆಯ ಮಿತಿಯೂ ಎಡಗಡೆಯ ಮಿತಿಯೂ ಬೇರೆ ಬೇರೆಯಾಗಿರಬಹುದು. ಜಿ (ಚಿ) ಅನಂತವಾಗಿದ್ದರೆ ವಿಚ್ಛಿನ್ನತೆ ಮೊದಲನೆಯ ಬಗೆಯದಾಗಿರುತ್ತದೆ ಅಥವಾ ಅದನ್ನು ಅನಂತ ವಿಚ್ಛಿನ್ನತೆ ಎನ್ನುತ್ತೇವೆ. ಉಳಿದ ಸಂದರ್ಭಗಳಲ್ಲಿ ವಿಚ್ಛಿನ್ನತೆ ಎರಡನೆಯ ಬಗೆಯದಾಗಿರುತ್ತದೆ ಎಂದು ಒಟ್ಟಾರೆ ಹೇಳಬಹುದು.)

1. ಉದಾಹರಣೆಗಳು : 1. , x=ಂ ಆದಾಗ ಇದಕ್ಕೆ ಬೆಲೆ ನಿರ್ಧೃತವಿಲ್ಲದುದರಿಂದ x=ಂ ಎಂಬಲ್ಲಿ ಉತ್ಪನ್ನ ವಿಚ್ಛಿನ್ನತೆ ಹೊಂದಿದೆ. ಆದರೆ ಉತ್ಪನ್ನವನ್ನು ಸ್ವಲ್ಪ ವ್ಯತ್ಯಾಸ ಮಾಡಿ , x‡ ಂ ಆದಾಗ, ಜಿ (ಂ) =ಂ ಎಂದು ಮಾಡಿದರೆ, ಆಗುತ್ತದೆ. ಆದ್ದರಿಂದ ಉತ್ಪನ್ನ ಈಗ ಎಲ್ಲ ಕಡೆಯೂ ಅವಿಚ್ಛಿನ್ನತೆ ಪಡೆದಿದೆ. ಈ ಕಾರಣದಿಂದ ಮೊದಲನೆಯ ಉತ್ಪನ್ನದಲ್ಲಿ x=ಂ ಎಂಬುದನ್ನು ತೆಗೆದುಹಾಕಬಹುದಾದ ವಿಚ್ಛಿನ್ನತೆ (ರಿಮೂವಬಲ್ ಡಿಸ್‍ಕಂಟಿನ್ಯೂಯಿಟಿ) ಎಂದು ಹೇಳುವುದುಂಟು.

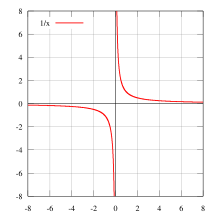
ಜಿ (x) = (1/x), x = ಂ ಅನಂತವಿಚ್ಛಿನ್ನತೆಯ ಬಿಂದು. ಮೇಲಿನ ಉತ್ಪನ್ನದಲ್ಲಿ x ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಯಾದಾಗ ಜಿ (x) = 1, ಇಲ್ಲದಿದ್ದರೆ ಜಿ (x) = ಂ. ಈ ಉತ್ಪನ್ನ x ನ ಎಲ್ಲ ಬೆಲೆಗಳಲ್ಲೂ ವಿಚ್ಛಿನ್ನತೆ ಪಡೆದಿದೆ.

ಜಿ (x) = . ಈಗ ; . ಆದ್ದರಿಂದ x = ಂ ವಿಚ್ಛಿನ್ನತೆಯ ಬಿಂದುವಾಗಿದೆ. ಚಲನಾಂಕ ಅಥವಾ ನಿಷ್ಪನ್ನ (ಡಿಫರೆನ್ಷಿಯಲ್ ಕೋಯಿಫಿಷೆಂಟ್; ಡಿರೈವೆಟಿವ್) ಇರಬೇಕಾದರೆ, ಜಿ (x) ಅವಿಚ್ಛಿನ್ನತೆಯನ್ನು ಪಡೆದಿರಬೇಕು. ವಿಚ್ಛಿನ್ನತೆಯಿದ್ದಲ್ಲಿ ನಿಷ್ಪನ್ನವಿರುವುದಿಲ್ಲ. ಆದರೆ ಅವಿಚ್ಛಿನ್ನತೆಯಿದ್ದ ಮಾತ್ರಕ್ಕೆ ನಿಷ್ಪನ್ನ ಇರುವುದೆಂಬ ನಿಯಮವೇನೂ ಇಲ್ಲ. ಮೇಲೆ ಕೊಟ್ಟಿರುವ , x ಂ ಆದಾಗ ಜಿ (ಂ) = ಂ ಎಂಬ ಉತ್ಪನ್ನ x = ಂ ಬಿಂದುವಿನಲ್ಲಿ ಅವಿಚ್ಛಿನ್ನತೆ ಪಡೆದಿದೆ. ಆದರೆ ಈ ಬಿಂದುಗಳ ಬಳಿ ನಿಷ್ಪನ್ನವಿಲ್ಲವೆಂಬುದನ್ನು ಗಮನಿಸಬಹುದು. ಉತ್ಪನ್ನ ನಕ್ಷೆ x = ಂ ಬಳಿ ಅನಂತ ಸಂಖ್ಯೆಯ ಆಂದೋಳನಕ್ಕೆ ಸಿಕ್ಕಿ ಮಿತಿಯಲ್ಲಿ ಮೂಲಬಿಂದುವಿಗೆ ಹೋಗಿ ಸೇರುವುದು. ಆದ್ದರಿಂದ ಮೂಲಬಿಂದುವಿನಲ್ಲಿ ನಿರ್ದಿಷ್ಟವಾದ ಸ್ಪರ್ಶರೇಖೆ ಇಲ್ಲ, ಎಂದರೆ ನಿಷ್ಪನ್ನವಿಲ್ಲ. ಹೀಗಾಗುವುದು ಈ ಒಂದು ಬಿಂದುವಿನಲ್ಲಿ ಮಾತ್ರ. x ನ ಇತರ ಬೆಲೆಗಳಿಗೆ ಏನೊಂದೂ ತೊಡಕೂ ಬರುವುದಿಲ್ಲ; ಅವಿಚ್ಛಿನ್ನತೆ ಮತ್ತು ನಿಷ್ಪನ್ನ ಇವೆ.

ಎಲ್ಲ ಕಡೆಯೂ ಅವಿಚ್ಛಿನ್ನತೆ ಪಡೆದು ಆದರೆ ಎಲ್ಲಿಯೂ ನಿಷ್ಪನ್ನ ಪಡೆಯದ ಒಂದು ಉತ್ಪನ್ನವನ್ನು ವಯರ್‍ಸ್ಟ್ರಾಸ್ ಮೊದಲು ರಚಿಸಿದ. ಮತ್ತು ಆಗುವಂತೆ b ಒಂದು ವಿಷಮ ಪೂರ್ಣಾಂಕ. ಈ ಉತ್ಪನ್ನಕ್ಕೆ ಮೇಲಿನ ಗುಣವಿದೆ. ಈ ಉತ್ಪನ್ನವನ್ನು ಹೊರಗೆಡವಿದಾಗ ಕ್ರಾಂತಿಕಾರಕವಾದ ಪರಿಣಾಮವಾಗಿ, ಗಣಿತ ಶಾಸ್ತ್ರಜ್ಞರಲ್ಲಿ ಉತ್ಪನ್ನಗಳು ಮತ್ತು ನಕ್ಷೆಗಳನ್ನು ಕುರಿತು ಅನೇಕ ಭಾವನೆಗಳು ತಿದ್ದುಪಡಿ ಹೊಂದಿದುವು. ವಯರ್‍ಸ್ಟ್ರಾಸ್‍ನ ಈ ಉತ್ಪನ್ನಕ್ಕೆ ನಕ್ಷೆಯೇ ಇಲ್ಲ.

ಈ ಉತ್ಪನ್ನವನ್ನು ಕಂಡುಹಿಡಿದ ಅನಂತರ ಇಂಥ ಮತ್ತು ಇನ್ನೂ ಇತರ ರೂಪಗಳುಳ್ಳ ಎಲ್ಲ ವಿಧದಲ್ಲಿಯೂ ಅವಿಚ್ಛಿನ್ನತೆಯನ್ನು ಪಡೆದು ಎಲ್ಲಿಯೂ ನಿಷ್ಪನ್ನವಿಲ್ಲದಿರುವ ಅನೇಕಾನೇಕ ಉತ್ಪನ್ನಗಳನ್ನು ರಚಿಸಿ, ಅವುಗಳ ಗುಣಗಳನ್ನು ವಿಮರ್ಶಿಸಿದ್ದಾರೆ.

ಅವಿಚ್ಛಿನ್ನತೆಯಿರುವ ಉತ್ಪನ್ನಗಳ ಗುಣಗಳು

ಕೆಳಗೆ ನಮೂದಿಸಿರುವ ಗುಣಗಳು ವಿಶ್ಲೇಷಣ ಗಣಿತದ ಅಧ್ಯಯನಕ್ಕೆ ಮೂಲಭೂತವಾಗಿದೆ.

1. ಪ್ರಮೇಯ 1: (ಚಿ,b) ಎಂಬ ಪರ್ಯಾಪ್ತ ಮತ್ತು ಮುಚ್ಚಿರುವ (ಕ್ಲೋಸ್ಡ್) ಅಂತರದಲ್ಲಿ ಜಿ(x) ಅವಿಚ್ಛಿನ್ನತೆ ಪಡೆದಿರಲಿ. ε ಯಾವುದೇ ಸಂಖ್ಯೆಯಾದರೆ, ಈ ಅಂತರದ ಯಾವುದೇ ಉಪಅಂತರದಲ್ಲಿ x1, x2 ಎರಡು ಬಿಂದುಗಳಾದರೆ, |ಜಿ(x1)-ಜಿ(x2)|<ε ಎಂಬ ಗುಣವಿರುವಂತೆ ಪರ್ಯಾಪ್ತ ಸಂಖ್ಯೆಯಿರುವ ಉಪ ಅವಧಿಗಳನ್ನು ಪಡೆಯುವುದು ಸಾಧ್ಯ.
2. ಪ್ರಮೇಯ 2: (ಚಿ,b) ಎಂಬ ಪರ್ಯಾಪ್ತ ಮತ್ತು ಮುಚ್ಚಿರುವ ಅಂತರದಲ್ಲಿ ಜಿ(x) ಅವಿಚ್ಛಿನ್ನತೆ ಪಡೆದಿದ್ದರೆ, ಈ ಅಂತರದಲ್ಲಿ ಜಿ(x)ಗೆ ಒಂದು ಖಚಿತ ಮೇಲುಗಡಿಯೂ (ಅಪ್ಪರ್ ಬೌಂಡ್) ಒಂದು ಖಚಿತ ಕೆಳಗಡಿಯೂ (ಲೋಯರ್ ಬೌಂಡ್) ಇರುತ್ತವೆ. ಆದ್ದರಿಂದ ಅಂತರದಲ್ಲಿ ಜಿ(x) ಪರ್ಯಾಪ್ತವಾಗಿದೆ. ಇದು ಮೊದಲನೆಯ ಪ್ರಮೇಯದ ಅನುಮಿತ.
3. ಪ್ರಮೇಯ 3: ಮೇಲೆ ತಿಳಿಸಿರುವ ಸಂಕೇತಗಳಿಂದ, ಯಾವುದೇ ಧನಸಂಖ್ಯೆ ε ದತ್ತವಾಗಿದ್ದರೆ, |x1-x2|<δ ಆದಾಗಲೆಲ್ಲ, |ಜಿ(x1)-ಜಿ(x2)|< ε ಆಗಿರುವಂತೆ, δ ಎಂಬ ಸಂಖ್ಯೆಯನ್ನು ಪಡೆಯುವುದು ಸಾಧ್ಯ. x1, x2 ಎಂಬಿವು (ಚಿ,b) ಅಂತರದ ಎರಡು ಬಿಂದುಗಳು. ಈ ಗುಣಕ್ಕೆ ಅವಿಚ್ಛಿನ್ನತೆಯ ಏಕಸಮತಾಗುಣ (ಯೂನಿಫಾರ್ಮಿಟಿ) ಎನ್ನುತ್ತೇವೆ. ಜಿ(x)ಗೆ (ಚಿ,b) ಅಂತರದಲ್ಲಿ ಅವಿಚ್ಛಿನ್ನತೆ ಇದ್ದರೆ ಅದು ಏಕಸಮತಾಗುಣದಿಂದಲೂ ಕೂಡಿರುತ್ತದೆ.
4. ಪ್ರಮೇಯ 4: (ಚಿ,b) ಎಂಬ ಪರ್ಯಾಪ್ತ ಮುಚ್ಚಿದ ಅಂತರದಲ್ಲಿ ಅವಿಚ್ಛಿನ್ನವಾಗಿರುವ ಉತ್ಪನ್ನ ಈ ಅಂತರದಲ್ಲಿ ಒಮ್ಮೆಯಾದರೂ ಅದರ ಮೇಲುಗಡಿಯ ಬೆಲೆಯನ್ನೂ, ಒಮ್ಮೆಯಾದರೂ ಕೆಳಗಡಿಯ ಬೆಲೆಯನ್ನೂ ಪಡೆಯುತ್ತದೆ.
5. ಪ್ರಮೇಯ5: ಪರ್ಯಾಪ್ತ ಮುಚ್ಚಿದ ಅಂತರ (ಚಿ,b)ಯಲ್ಲಿ ಅವಿಚ್ಛಿನ್ನವಾಗಿರುವ ಜಿ(x) ಉತ್ಪನ್ನ ಈ ಅವಧಿಯಲ್ಲಿ ಜಿ(ಚಿ)ಗೂ ಜಿ(b)ಗೂ ನಡುವೆ ಇರುವ ಯಾವ ಸಂಖ್ಯೆಯನ್ನೇ ಆಗಲಿ ಒಮ್ಮೆಯಾದರೂ ಪಡೆಯುತ್ತದೆ. ಇದರ ಒಂದು ಅನುಮಿತ ಸಮೀಕರಣ ಸಿದ್ಧಾಂತದಲ್ಲಿ ಬಹುಮುಖ್ಯವಾದುದು.
6. ಪ್ರಮೇಯ 6: ಜಿ(ಚಿ)>0, ಜಿ(b)<0 ಆಗಿದ್ದರೆ, ಮೇಲಿನ ನಿಯಮಗಳಿರುವ ಜಿ(x)=0 ಎಂಬ ಸಮೀಕರಣಕ್ಕೆ (ಚಿ,b) ಅಂತರದಲ್ಲಿ ಕನಿಷ್ಟಪಕ್ಷ ಒಂದು ಮೂಲವಾದರೂ ಇರುತ್ತದೆ. ಒಂದಕ್ಕಿಂತ ಹೆಚ್ಚು ಮೂಲಗಳಿದ್ದರೆ, ಇವು ವಿಷಮ ಸಂಖ್ಯೆಯಲ್ಲಿರುತ್ತವೆ ಎಂದು ತೋರಿಸಬಹುದು.

ಹಿಂದೆಯೇ ತಿಳಿಸಿರುವಂತೆ ನಿಷ್ಪನ್ನವಿರಬೇಕಾದರೆ ಅವಿಚ್ಛಿನ್ನತೆ ಆವಶ್ಯಕವಾದ ಅಥವಾ ಬೇಕಾದ (ನೆಸಸ್ಸರಿ) ನಿಯಮ. ಚಲನಕಲನಶಾಸ್ತ್ರದ (ಡಿಫರೆನ್ಷಿಯಲ್ ಕ್ಯಾಲ್ಕುಲಸ್) ಬೆಳೆವಣಿಗೆ ಅವಿಚ್ಛಿನ್ನತಾಗುಣವಿರುವ ಉತ್ಪನ್ನಗಳಿಗೇ ಸೇರಿದ್ದು ಎಂದು ಹೇಳಬೇಕಾದ್ದಿಲ್ಲ. ಇದರ ಜೊತೆಗೆ ಪ್ರಥಮ ನಿಷ್ಪನ್ನದ, ದ್ವಿತೀಯ ನಿಷ್ಪನ್ನದ ಇತ್ಯಾದಿಗಳ ಅವಿಚ್ಛಿನ್ನತೆಯನ್ನು ಸಮಯೋಚಿತವಾಗಿ ಒಪ್ಪಿಕೊಂಡು, ಶಾಸ್ತ್ರ ಬೆಳೆದಿದೆ. ತಳಹದಿಯ ರೂಪದಲ್ಲಿರುವ ಒಂದು ಪ್ರಮೇಯವನ್ನು ಮಾತ್ರ ಇಲ್ಲಿ ಕೊಡಲಾಗಿದೆ.

1. ರೋಲನ ಪ್ರಮೇಯ: (ಚಿ,b) ಎಂಬ ಪರ್ಯಾಪ್ತ ಮತ್ತು ಮುಚ್ಚಿದ ನಂತರದಲ್ಲಿ ಜಿ(x) ಅವಿಚ್ಛಿನ್ನವಾಗಿದ್ದು ಇದೇ ಅಂತರದಲ್ಲಿ (ಅವಶ್ಯವಿದ್ದರೆ ಅಂತಿಮ ಬಿಂದುಗಳಾದ ಚಿ,b, ಗಳನ್ನು ಬಿಟ್ಟು) ಜಿ'(x) ಪರ್ಯಾಪ್ತವಾಗಿದ್ದರೆ, ಆಗ ಈ ಅಂತರದಲ್ಲಿ ಜಿ'(x)=0 ಆಗುವ ಹಾಗೆ xಗೆ ಒಂದಾದರೂ ಬೆಲೆಯಿರುತ್ತದೆ.

ಸಮಾಸಫಲ ಅಥವಾ ಸಮಾಸೀಯ (ಇಂಟೆಗ್ರಲ್)

ಪರ್ಯಾಪ್ತ ಅವಧಿಯಲ್ಲಿ ಪರ್ಯಾಪ್ತ ಉತ್ಪನ್ನವಾದ ಜಿ(x)ಗೆ ಸಮಾಸೀಯವಿರಲು ಎಂದರೆ ಚಿ∫b ಜಿ(x) ಜx ಇದು ನಿರ್ಧೃತವಾಗಿರಲು, ಜಿ(x)ನ ಅವಿಚ್ಛಿನ್ನತೆ ಸಾಕಾಗುವ (ಸಫಿಷಿಯೆಂಟ್) ಗುಣ ಬೇಕಾಗುವ ಗುಣವಾಗುವುದಿಲ್ಲ. ಅಲ್ಲಲ್ಲೇ ವಿಚ್ಛಿನ್ನತೆಗಳಿದ್ದರೂ ಸಮಾಸೀಯವಿರಲು ಸಾಧ್ಯ.

1. ಎರಡು ಅಥವಾ ಅನೇಕ ಚರಗಳಿರುವ ಉತ್ಪನ್ನಗಳ ಅವಿಚ್ಛಿನ್ನತೆಯನ್ನು ಮೇಲಿನ ಭಾವನೆಗಳನ್ನೇ ವಿಸ್ತರಿಸಿ ವ್ಯಾಖ್ಯೆ ಮಾಡಬಹುದು.

ವ್ಯಾಖ್ಯೆ : ದತ್ತ ಧನಸಂಖ್ಯೆ ಮತ್ತು ಆಗಿ ಇರುವಂಥ ಎಲ್ಲ x,ಥಿ ಬೆಲೆಗಳಿಗೂ ಎಂಬ ಗುಣವಿದ್ದರೆ, ಜಿ(x,ಥಿ) ಉತ್ಪನ್ನ (ಚಿ,b) ಬಿಂದುವಿನಲ್ಲಿ ಅವಿಚ್ಫಿನ್ನತೆ ಪಡೆದಿರುವುದು. ಈ ಗುಣ ಒಂದು ಪ್ರದೇಶ ಖನ ಎಲ್ಲ ಬಿಂದುಗಳಿಗೂ ಇದ್ದರೆ. ಜಿ(x,ಥಿ) ಉತ್ಪನ್ನ ಖ ಪ್ರದೇಶದಲ್ಲಿ ಅವಿಚ್ಫಿನ್ನತೆಯನ್ನು ಪಡೆದಿರುವುದು.

ಮೇಲೆ ವಿವರಿಸಿರುವ 1-5ರವರೆಗಿನ ಪ್ರಮೇಯಗಳನ್ನು ಅದೇ ರೀತಿಯ ವಿಧಾನಗಳಿಂದ ಎರಡು ಅಥವಾ ಹೆಚ್ಚು ಚರಗಳಿರುವ ಉತ್ಪನ್ನಗಳಿಗೆ ವಿಸ್ತರಿಸಬಹುದು.